About Me

---

I am Xinyu Chen (陈新宇), an Assistant Professor at the University of Central Florida (UCF) since January 2026. My research focuses on developing theoretical and interpretable machine learning methods for modeling spatiotemporal data and computational social science data. The model development from a machine learning perspective can be summarized as tensor computations for machine learning (Tensor4ML) and optimization for interpretable machine learning (Opt4ML). In practice, the spatiotemporal datasets are often multidimensional tensors, including human mobility, trajectory data, traffic flow, fluid flow, climate/weather variable data, energy consumption, and international trade data. Our work addresses key scientific problems in computational engineering such as:

• Spatiotemporal data imputation & prediction: Imputing and forecasting spatiotemporal traffic data (e.g., urban traffic states, origin-destination flow) in the presence of missing values.
  • Bayesian temporal factorization for multidimensional time series prediction (TPAMI 2022)
  • Forecasting urban traffic states with sparse data using Hankel temporal matrix factorization (IJOC 2024)
  • Forecasting sparse movement speed of urban road networks with nonstationary temporal matrix factorization (TS 2025)
  

  Keywords: Matrix decomposition; Tensor decomposition; Time series autoregression; Hankel matrix; Bayesian inference (e.g., MCMC); Conjugate gradient.
  Highlight: Integrating vector autoregression of temporal factor matrix into matrix and tensor factorization.



• Speed field reconstruction of traffic flow: Generating vehicular speed fields from partially observed trajectory data.
  • Laplacian convolutional representation for traffic time series imputation (TKDE 2024)
  

  Keywords: Circulant matrix; Nuclear norm minimization; Laplacian regularization; Fast Fourier transform.
  Highlight: Accelerating the optimization of time series reconstruction with convolution and fast Fourier transform.



• Spatiotemporal pattern discovery: Discovering dynamic patterns from urban human mobility, international trade, and climate systems.
  • Discovering dynamic patterns from spatiotemporal data with time-varying low-rank autoregression (TKDE 2024)
  • Dynamic autoregressive tensor factorization for pattern discovery of spatiotemporal systems (TPAMI 2025)
  

  Keywords: Tensor decomposition; Time series autoregression; Dynamic mode decomposition; Orthogonal Procrustes problem; Conjugate gradient.
  Highlight: Identifying interpretable low-rank decomposition of spatiotemporal time-varying autoregression.








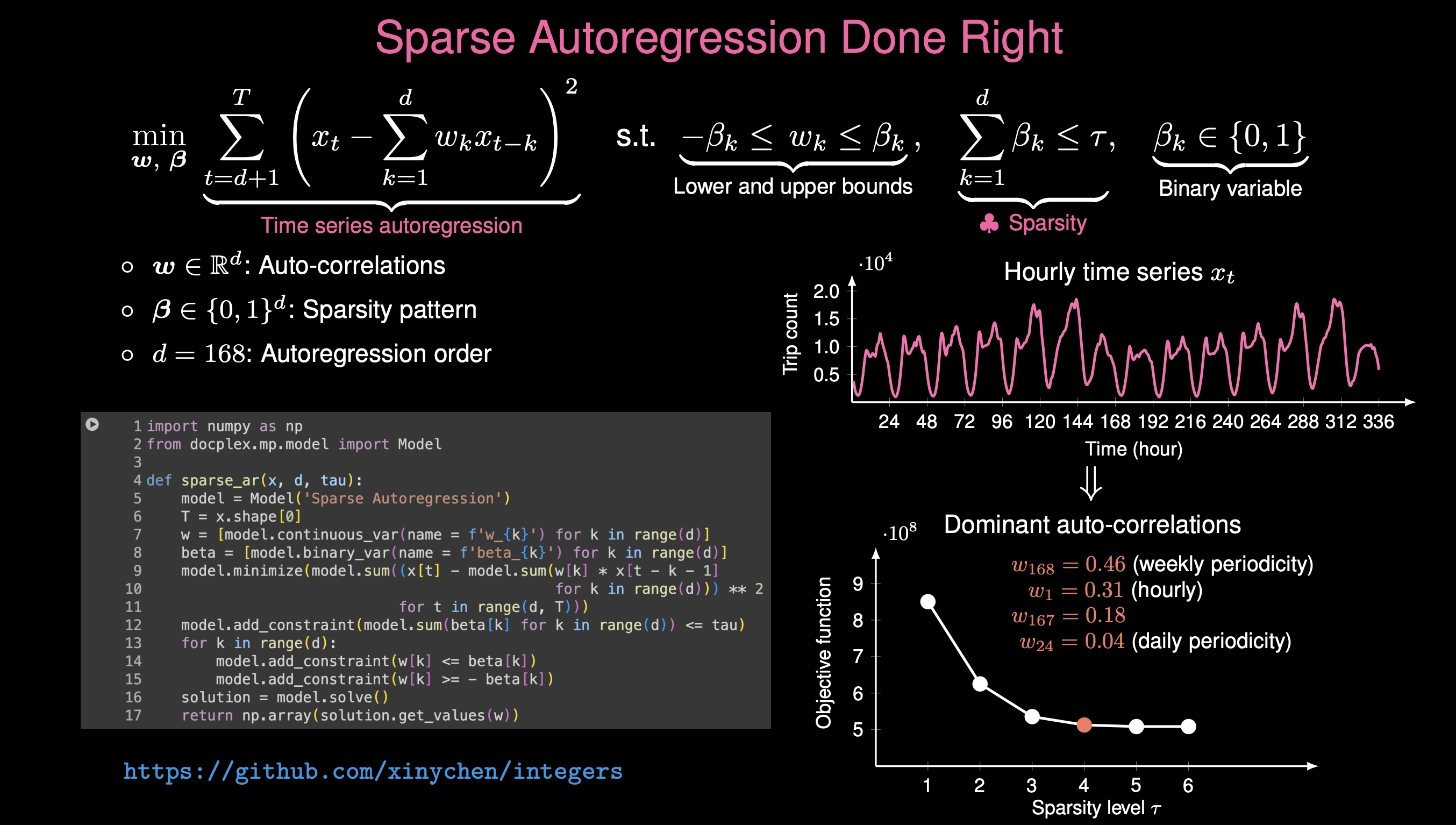
• Time series periodicity quantification: Quantifying periodicity and seasonality of urban human mobility (i.e., daily/weekly regularity) and climate systems (i.e., yearly seasonality). Periodicity is key to time measurement.
  • Correlating time series with interpretable convolutional kernels (TKDE 2025)
  • Interpretable time series autoregression for periodicity quantification
  • Data-driven discovery of mobility periodicity for understanding urban systems
  

  Keywords: Interpretable machine learning; Time series autoregression; Sparse \(\ell_0\)-norm optimization; Subspace pursuit; Mixed-integer optimization.
  Highlight: Reformulating \(\ell_0\)-norm induced sparse autoregression of time series as a mixed-integer optimization problem.








• Causal discovery from structured data (new)
  

Until now, our research work has been published in top-tier scientific journals such as:

• IEEE journals: IEEE Transactions on Knowledge and Data Engineering (TKDE), IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI).

• INFORMS journals: INFORMS Journal on Computing (IJOC), Transportation Science (TS).

Prior to joining UCF, I was a Postdoctoral Associate at MIT from 2024 to 2025, working with Prof. Jinhua Zhao on data-driven machine learning in computational engineering. At MIT, I was involved in the Mens, Manus, and Machina (M3S) and Department of Energy (DOE) projects. I completed my PhD degree in 2023 at the University of Montreal in Canada, supervised by Prof. Nicolas Saunier. My PhD research project was conducted under the support of the IVADO PhD Excellence Scholarship ($100k) and CIRRELT PhD Excellence Scholarship ($5k). My doctoral thesis, “Matrix and Tensor Models for Spatiotemporal Traffic Data Imputation and Forecasting,” laid the foundation for my ongoing research.

As a strong advocate of open-source and reproducible research, I actively share datasets, Python codes, and tutorials on GitHub and consider how to make tangible contributions to the research community. I lead several innovative projects, including transdim (machine learning for transportation data imputation and prediction, 1.3k+ stars) and awesome-latex-drawing (academic drawing examples in LaTeX, 1.8k+ stars), with 700+ GitHub followers and 5.5k+ stars in total. I am now leading the Spatiotemporal Data Computing project (5k+ unique visitors) on GitHub and regularly updating the tutorials related to data science & machine learning:

• Time Series Modeling: Time series convolution

• LaTeX Visualization: Awesome LaTeX drawing

• Interactive Visualization Tools: Time series periodicity

Driven by the philosophy of “大道至简” (make it as simple and clear as possible), I strive to bridge theoretical advancements in applied mathematics, machine learning, and optimization with real-world engineering applications, contributing to fields such as intelligent transportation systems, urban science, and AI for science (please check out our Knowledge Repository). Our research continues to push the boundaries of data science, machine learning, and computational engineering, addressing complex challenges across academia and industry.

Archive

---

vistors & views since September 2021