About Me


I am Xinyu Chen (陈新宇), a Postdoctoral Associate at MIT, working with Prof. Jinhua Zhao on data-driven machine learning in computational engineering. I am currently involved in the Mens, Manus, and Machina (M3S) and Department of Energy (DOE) projects. My research focuses on developing theoretical and interpretable machine learning methods for modeling spatiotemporal data and computational social science data. The model development from a machine learning perspective can be summarized as tensor computations for machine learning (Tensor4ML) and optimization for interpretable machine learning (Opt4ML). In practice, the spatiotemporal datasets are often multidimensional tensors, including human mobility, trajectory data, traffic flow, fluid flow, climate/weather variable data, energy consumption, and international trade data. Our work addresses key scientific problems in computational engineering such as:

  • Spatiotemporal data imputation & prediction: Imputing and forecasting spatiotemporal traffic data (e.g., urban traffic states, origin-destination flow) in the presence of missing values.
    • Bayesian temporal factorization for multidimensional time series prediction (TPAMI 2022)
    • Forecasting urban traffic states with sparse data using Hankel temporal matrix factorization (IJOC 2024)
    • Forecasting sparse movement speed of urban road networks with nonstationary temporal matrix factorization (TS 2025)

    Keywords: Matrix decomposition; Tensor decomposition; Time series autoregression; Hankel matrix; Bayesian inference (e.g., MCMC)

    Highlight: Integrating vector autoregression of temporal factor matrix into matrix and tensor factorization.
    • $$ \min_{\boldsymbol{W},\,\boldsymbol{X},\,\boldsymbol{A}}\, \underbrace{\frac{1}{2}\|\mathcal{P}_{\Omega}(\boldsymbol{Y}-\boldsymbol{W}^\top\boldsymbol{X})\|_{F}^{2}}_{\color{red}\text{Matrix factorization}}+ \underbrace{\frac{\gamma}{2}\sum_{t=d+m+1}^{T}\Bigl\| \underbrace{(\boldsymbol{x}_{t}-\boldsymbol{x}_{t-m})}_{\color{blue}\text{Differencing}}- \sum_{k=1}^{d}\boldsymbol{A}_{k} \underbrace{(\boldsymbol{x}_{t-k}-\boldsymbol{x}_{t-m-k})}_{\color{blue}\text{Differencing}} \Bigr\|_2^2}_{\color{red}\clubsuit\,\text{Nonstationary autoregression}} $$

  • Speed field reconstruction of traffic flow: Generating vehicular speed fields from partially observed trajectory data.
    • Laplacian convolutional representation for traffic time series imputation (TKDE 2024)

    Keywords: Circulant matrix; Nuclear norm minimization; Laplacian regularization; Fast Fourier transform

    Highlight: Accelerating the optimization of time series reconstruction with convolution and fast Fourier transform.
    • $$ \min_{\boldsymbol{x}}\,\,\underbrace{\|\mathcal{C}(\boldsymbol{x})\|_{*}}_{\color{red}\text{Nuclear norm}}+\underbrace{\frac{\gamma}{2}\|\boldsymbol{\ell}\star\boldsymbol{x}\|_2^2}_{\color{red}\clubsuit\,\,\text{Laplacian regularization}}\quad\text{s.t.}\,\,\underbrace{\|\mathcal{P}_{\Omega}(\boldsymbol{x}-\boldsymbol{y})\|_2\leq\epsilon}_{\color{blue}\text{Partial observations in}\,\boldsymbol{y}} $$

  • Spatiotemporal pattern discovery: Discovering dynamic patterns from urban human mobility, international trade, and climate systems.
    • Discovering dynamic patterns from spatiotemporal data with time-varying low-rank autoregression (TKDE 2024)
    • Dynamic autoregressive tensor factorization for pattern discovery of spatiotemporal systems (TPAMI 2025)

    Keywords: Tensor decomposition; Time series autoregression; Dynamic mode decomposition; Orthogonal Procrustes problem

    Highlight: Identifying interpretable low-rank decomposition of spatiotemporal time-varying autoregression.
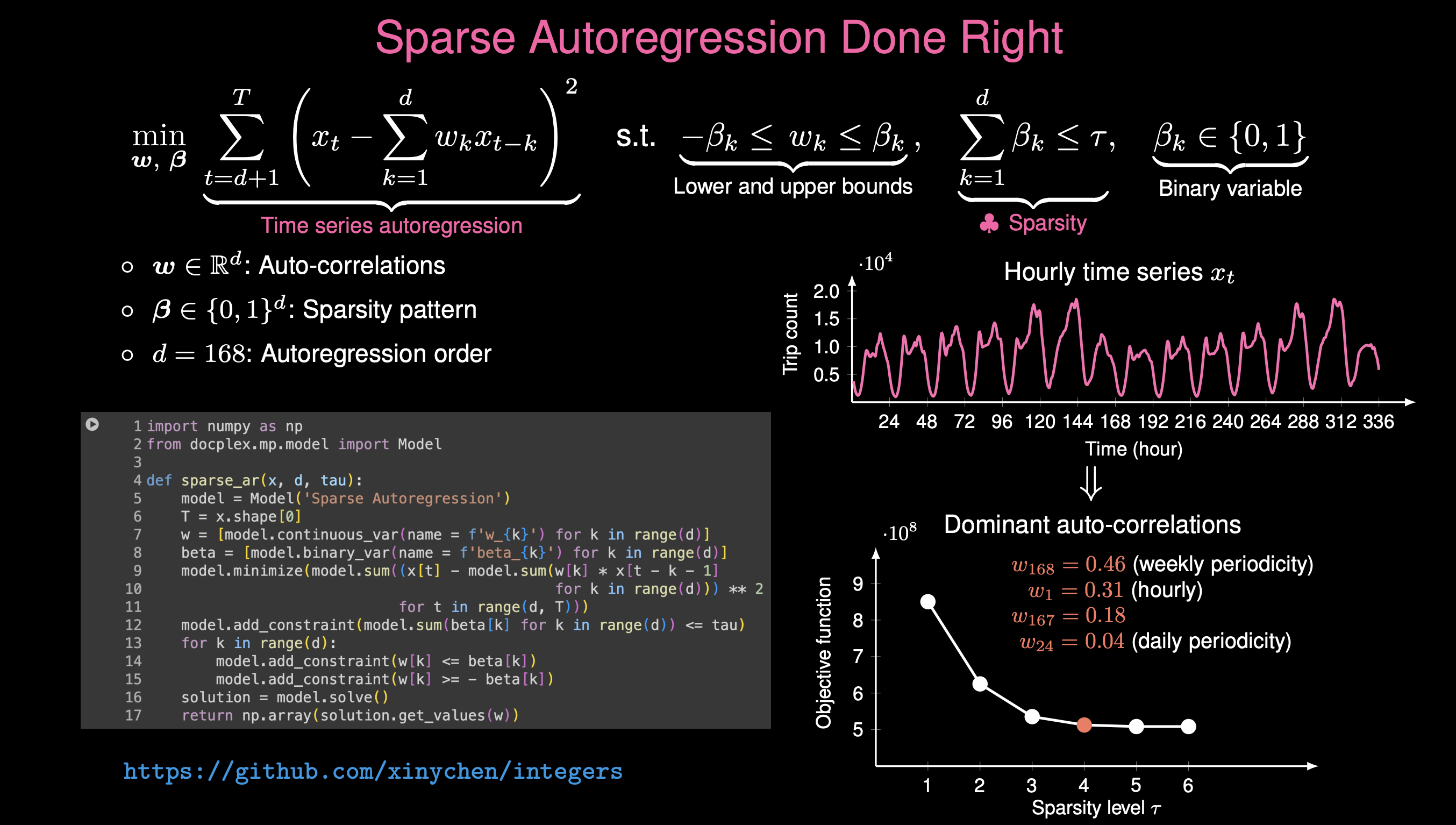
    • $$ \min_{\boldsymbol{\mathcal{G}},\,\boldsymbol{W},\,\boldsymbol{V},\,\boldsymbol{X}}\,\,\underbrace{\sum_{t=1}^{T-1}\bigl\|\boldsymbol{y}_{t+1}-\underbrace{(\boldsymbol{\mathcal{G}}\times_{1}\boldsymbol{W}\times_{2}\boldsymbol{V}\times_{3}\boldsymbol{x}_{t}^{\top})}_{\color{red}\clubsuit\,\,\color{blue}\text{Tensor decomposition}}\boldsymbol{y}_{t}\bigr\|_{2}^{2}}_{\color{red}\text{Time-varying autoregression}}\quad\text{s.t.}\,\,\underbrace{\boldsymbol{W}^{\top}\boldsymbol{W}=\boldsymbol{I}}_{\color{red}\clubsuit\,\,\color{blue}\text{Orthogonality}} $$

  • Time series periodicity quantification: Quantifying periodicity and seasonality of urban human mobility (i.e., daily/weekly regularity) and climate systems (i.e., yearly seasonality). Periodicity is key to time measurement.
    • Correlating time series with interpretable convolutional kernels (TKDE 2025)
    • Interpretable time series autoregression for periodicity quantification
    • Data-driven discovery of mobility periodicity for understanding urban systems

    Keywords: Interpretable machine learning; Time series autoregression; Sparse \(\ell_0\)-norm optimization; Subspace pursuit; Mixed-integer optimization

    Highlight: Reformulating \(\ell_0\)-norm induced sparse autoregression of time series as a mixed-integer optimization problem.
    • $$ \min_{\boldsymbol{w},\,\boldsymbol{\beta}}\,\,\underbrace{\sum_{t=d+1}^{T}\left(x_{t}-\sum_{k=1}^{d}w_{k}x_{t-k}\right)^2}_{\color{red}\text{Time series autoregression}}\quad\text{s.t.}\,\,\underbrace{-\alpha\cdot\beta_{k}\leq\,w_{k}\leq\alpha\cdot\beta_{k}}_{\color{blue}\text{Lower and upper bounds}},\,\,\,\underbrace{\sum_{k=1}^{d}\beta_{k}\leq\tau}_{\color{red}\clubsuit\,\,\color{blue}\text{Sparsity}},\,\,\,\underbrace{\beta_{k}\in\{0,1\}}_{\color{blue}\text{Binary variable}} $$

  • Causal discovery from structured data (new)

Note: Methodological contributions are highlighted by \(\color{red}\clubsuit\).


Prior to joining MIT, I completed my PhD degree at the University of Montreal in Canada, supervised by Prof. Nicolas Saunier. My PhD research project was conducted under the support of the IVADO PhD Excellence Scholarship ($100k) and CIRRELT PhD Excellence Scholarship ($5k). My doctoral thesis, “Matrix and Tensor Models for Spatiotemporal Traffic Data Imputation and Forecasting”, laid the foundation for my ongoing research. Until now, our research work has been published in top-tier scientific journals such as: As a strong advocate of open-source and reproducible research, I actively share datasets, Python codes, and tutorials on GitHub and consider how to make tangible contributions to the research community. I lead several innovative projects, including transdim (machine learning for transportation data imputation and prediction, 1.3k+ stars) and awesome-latex-drawing (academic drawing examples in LaTeX, 1.8k+ stars), with 600+ GitHub followers and 5.5k+ stars in total. I am now leading the Spatiotemporal Data Computing project (4k+ unique visitors) on GitHub and regularly updating the tutorials related to data science & machine learning:
Driven by the philosophy of “大道至简” (make it as simple and clear as possible), I strive to bridge theoretical advancements in applied mathematics, machine learning, and optimization with real-world engineering applications, contributing to fields such as intelligent transportation systems, urban science, and AI for science. Our research continues to push the boundaries of data science, machine learning, and computational engineering, addressing complex challenges across academia and industry.

Selected News

(For the full list of news, please check out the News tab.)

Archive

vistors & views since September 2021

drawing
drawing
drawing